Pasos Simples para integrar por partes
1.-Encontrar U y su respectiva derivada
2.-En estos casos la derivadade V se encuentra directa (simplemente es la parte que se queda de la integral su producto derivable seguramente esta en el formulario, ya sea U ala n o E con exponencial u
3.-se aplica la formula de integracion por partes
4.-Se realizan las operaciones restantes (iniciando con las que se encuentran en parentesis)
5.-Se obtiene el resultado final
miércoles, 27 de mayo de 2009
Si tenemos dos funciones u=u(x) y v=v(x) las cuales reconocemos que son diferenciables podemos determinar
las propiedades de las diferenciales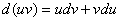
notemos que en la igualdad se tiene una integración casi del mismo tipo, observemos que sucede si intentamos la integración:
nuevamente integrando por partes tenemos en la elección:
sustituyendo tenemos:
sustituyendo tendremos en la ecuación original tendremos:
despejando
del segundo término tendremos:
despejando finalmente tendremos:
las propiedades de las diferenciales
integrando esta igualdad tenemos:
pero recordemos que
pero recordemos que
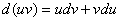
por lo que:
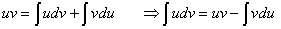
lo cual representa un importante resultado que garantiza, que siempre y cuando dos funciones sean diferenciables, podemos utilizar el artificio, conocido como integración por partes:
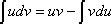
1. Ejemplos:
Integral la función
Solución:
No tenemos el diferencial para poder determinar de forma inmediata la integración sin embargo:
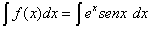
si tomamos:
lo cual aplicando la ecuación de la integración por partes tendremos:
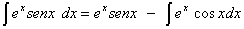
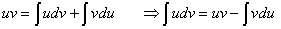
lo cual representa un importante resultado que garantiza, que siempre y cuando dos funciones sean diferenciables, podemos utilizar el artificio, conocido como integración por partes:
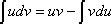
1. Ejemplos:
Integral la función
Solución:
No tenemos el diferencial para poder determinar de forma inmediata la integración sin embargo:
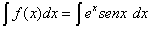
si tomamos:
lo cual aplicando la ecuación de la integración por partes tendremos:
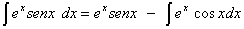
notemos que en la igualdad se tiene una integración casi del mismo tipo, observemos que sucede si intentamos la integración:
nuevamente integrando por partes tenemos en la elección:
sustituyendo tenemos:
sustituyendo tendremos en la ecuación original tendremos:
despejando
del segundo término tendremos:
despejando finalmente tendremos:
Que Es el calculo integral?
El cálculo integral,también conocido como cálculo infinitesimal es una rama de las matemáticas en la cual se estudia el cálculo a partir del proceso de integración o antiderivación, es muy común en la ingeniería y en la matemática en general y se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, Descartes, Newton y Barrow, éste último fue el que junto con aportes de Newton, crearon el Teorema Fundamental dee Calculo integral que propone que la derivación y la integración son procesos inversos.
Fue usado por primera vez por científicos como Arquímedes, Descartes, Newton y Barrow, éste último fue el que junto con aportes de Newton, crearon el Teorema Fundamental dee Calculo integral que propone que la derivación y la integración son procesos inversos.
lunes, 25 de mayo de 2009
Calculo Integral
GLOSARIO
DERIVADA:
Es Una Razon de cambio de 2 magnitudes , tambien hay que recordar que la derivada de una funcion Y=f(x) se define como un limite. Para sacar la variable de una funcion se requiere identificar a la variable y a su constante, en la mayoria de los casos la variable suele ser X,Y,Z tambien se puede usar M,N o cualquier letra pero las ultimas letras del abecedario son las mas comunes.
Para identificar las constantes suelen ser principalmente las letras A,B o C o por numeros
Ejemplo:
4xdx=4dx
24xdx=24dx
En este caso la variable es X y la constante son 4 y 24, la variable siempre tendra el valo de 1 a no ser que este elevado a una potencia
Ejemplo:
3x6=Siendo 6 el exponente su derivada seria:
18x5 (siendo 5 el exponente) ya que el numero al que se eleva la pótencia (en este caso es 6) se multiplica por el valor de la constante 3x (en este caso el valor es 3) [3x6=18] y se le resta 1 al exponente. [6-1=5 exponente] dando como resultado
la derivada
dy:3x6= 18x5
dy:2x4=8x3
dy=15x2=30x
DIFERENCIAL:
el diferencial (dx, dy, dt, etc...) de una función representa un cambio infinitamente pequeño en su valor. y se representa por
∫
DERIVADA:
Es Una Razon de cambio de 2 magnitudes , tambien hay que recordar que la derivada de una funcion Y=f(x) se define como un limite. Para sacar la variable de una funcion se requiere identificar a la variable y a su constante, en la mayoria de los casos la variable suele ser X,Y,Z tambien se puede usar M,N o cualquier letra pero las ultimas letras del abecedario son las mas comunes.
Para identificar las constantes suelen ser principalmente las letras A,B o C o por numeros
Ejemplo:
4xdx=4dx
24xdx=24dx
En este caso la variable es X y la constante son 4 y 24, la variable siempre tendra el valo de 1 a no ser que este elevado a una potencia
Ejemplo:
3x6=Siendo 6 el exponente su derivada seria:
18x5 (siendo 5 el exponente) ya que el numero al que se eleva la pótencia (en este caso es 6) se multiplica por el valor de la constante 3x (en este caso el valor es 3) [3x6=18] y se le resta 1 al exponente. [6-1=5 exponente] dando como resultado
la derivada
dy:3x6= 18x5
dy:2x4=8x3
dy=15x2=30x
DIFERENCIAL:
el diferencial (dx, dy, dt, etc...) de una función representa un cambio infinitamente pequeño en su valor. y se representa por
∫
Suscribirse a:
Entradas (Atom)